联系我们
与泰克代表实时聊天。 工作时间:上午 9:00 - 下午 5:00(太平洋标准时间)。
电话
致电我们
工作时间:上午9:00-下午5:00(太平洋标准时间)
下载
下载手册、产品技术资料、软件等:
反馈
User Defined Filter Tool
5/6 Series B MSO, 7 Series DPO Option 5-UDFLT, 6-UDFLT, and 7-UDFLT Application Datasheet
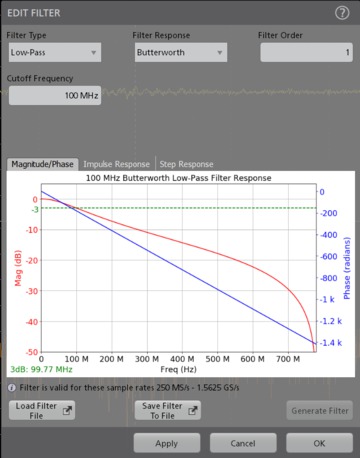
5/6 Series B MSO, 7 Series DPO Option 5-UDFLT, 6-UDFLT, and 7-UDFLT Application Datasheet
Download the Datasheet PDF file available above to learn more about the User Defined Filter Tool.

